Integration by Adaptive Simpson method of a function on a semi-infinite interval, based on iads() More...

Detailed Description

Integration by Adaptive Simpson method of a function on a semi-infinite interval, based on iads()

The routine calculates an approximation 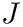to a definite integral

$J \approx I =\int_{a}^{\infty} f(x, args) dx$

hopefully satisfying

$|| I - J || \le \max ( epsabs, epsrel \cdot ||I|| ).$

Parameters

[in]	f	The function to integrate
[in]	a	(real) lower limit of integration
[in]	brkpts	(real, array) Break points where the integration domain will be split
[in]	args	(real, array, optional) extra arguments (if needed) to be passed to the function `f`
[out]	IntVal	(same kind as `f`) Approximation to integral
[in]	epsabs	(real, optional) Absolute accuracy requested. Default = 1.e-7
[in]	epsrel	(real, optional) Relative accuracy requested. Default = 1.e-5
[out]	abserr	(real, optional) Estimation of absolute error achieved
[out]	neval	(integer, optional) Number of function evaluations performed
[out]	ier	(integer, optional) Error code

The documentation for this interface was generated from the following file: