NuMFor 9f2ab49 (2024-04-08)
Numerical (Modern) Fortran. Library for Simple Numerical computing
Public Member Functions | Public Attributes | List of all members
cubicspline Interface Reference

Type used to keep all information on splines. More...

Public Member Functions

procedure, pass(csp) cspl_interp (xc, csp)
 Interpolates a function using previously calculated representation of splines.
 
procedure, pass(csp) cspl_interp_tab (xnew, csp)
 Interpolates a function using previously calculated representation of splines. Works over an array of x values and returns an array of interpolated values
 
generic evaluate (xc, csp)
 Interpolates a function using previously calculated representation of splines.
 
generic evaluate (xnew, csp)
 Interpolates a function using previously calculated representation of splines. Works over an array of x values and returns an array of interpolated values
 
procedure, pass(csp) cspl_interpdev (xc, csp, m)
 Interpolates the first derivative of a function.
 
procedure, pass(csp) cspl_interpdev_tab (xnew, csp, m)
 
generic derivative (xc, csp, m)
 Interpolates the first derivative of a function.
 
generic derivative (xnew, csp, m)
 
procedure, pass(csp) integrate (xl, xu, csp, extrapolate)
 Definite integral of a cubic spline function.
 
procedure, pass(csp) roots (csp)
 csplroots Computes the roots of the Spline approximation
 
type(cubicspline) function init (x, y, s1, sn)
 

Public Attributes

real(dp), dimension(:, :), allocatable s
 Coefficients of the polynomial S(:,i) valid for each interval i, x(i) <= x < x(i+1)
 
real(dp), dimension(:), allocatable x
 Limits of the intervals.
 

Detailed Description

Type used to keep all information on splines.

CubicSpline is the OO interface to cubic splines interpolation.

For each interval, the value will be 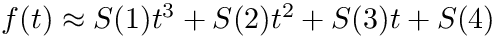$f(t) \approx S(1) t^3 + S(2) t^2 + S(3) t + S(4)$ where $t = x - x_{i}$ is the distance to the nearest point on the left.

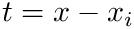
Example:

! Create the CubicSpline
! Notice that we know exactly the second derivative
csp = cubicspline(x, y, -y(1), -y(ndim))
! Apply the interpolation to the new grid
ynew = csp%evaluate(xnew)

And to evaluate the derivative

! Given a CubicSpline object csp, evaluate the derivative
yder = csp%derivative(xnew)

Member Function/Subroutine Documentation

◆ cspl_interp()

procedure, pass(csp) cspl_interp ( real(dp), intent(in) xc,
class(cubicspline), intent(in) csp )

Interpolates a function using previously calculated representation of splines.

Note
Before calling this function, must be called csplrep()
Parameters
[in]xcvalue where evaluate the interpolation
[in]cspspline coefficients
Returns
the interpolated value

◆ cspl_interp_tab()

procedure, pass(csp) cspl_interp_tab ( real(dp), dimension(:), intent(in) xnew,
class(cubicspline), intent(in) csp )

Interpolates a function using previously calculated representation of splines. Works over an array of x values and returns an array of interpolated values

Parameters
[in]cspspline coefficients
[in]xnewarray of x values
Returns
Interpolated values at xnew positions

◆ cspl_interpdev()

procedure, pass(csp) cspl_interpdev ( real(dp), intent(in) xc,
class(cubicspline), intent(in) csp,
integer, intent(in), optional m )

Interpolates the first derivative of a function.

Note
Before calling this function, must be called csplrep()
Parameters
[in]xcvalue where evaluate the interpolation
[in]cspspline coefficients
[in]morder of derivation
Returns
the interpolated value

◆ cspl_interpdev_tab()

procedure, pass(csp) cspl_interpdev_tab ( real(dp), dimension(:), intent(in) xnew,
class(cubicspline), intent(in) csp,
integer, intent(in), optional m )
Parameters
[in]cspspline coefficients
[in]xnewarray of x values
Returns
Interpolated values
Parameters
[in]morder of derivative

◆ derivative() [1/2]

generic derivative ( real(dp), intent(in) xc,
class(cubicspline), intent(in) csp,
integer, intent(in), optional m )

Interpolates the first derivative of a function.

Note
Before calling this function, must be called csplrep()
Parameters
[in]xcvalue where evaluate the interpolation
[in]cspspline coefficients
[in]morder of derivation
Returns
the interpolated value

◆ derivative() [2/2]

generic derivative ( real(dp), dimension(:), intent(in) xnew,
class(cubicspline), intent(in) csp,
integer, intent(in), optional m )
Parameters
[in]cspspline coefficients
[in]xnewarray of x values
Returns
Interpolated values
Parameters
[in]morder of derivative

◆ evaluate() [1/2]

generic evaluate ( real(dp), intent(in) xc,
class(cubicspline), intent(in) csp )

Interpolates a function using previously calculated representation of splines.

Note
Before calling this function, must be called csplrep()
Parameters
[in]xcvalue where evaluate the interpolation
[in]cspspline coefficients
Returns
the interpolated value

◆ evaluate() [2/2]

generic evaluate ( real(dp), dimension(:), intent(in) xnew,
class(cubicspline), intent(in) csp )

Interpolates a function using previously calculated representation of splines. Works over an array of x values and returns an array of interpolated values

Parameters
[in]cspspline coefficients
[in]xnewarray of x values
Returns
Interpolated values at xnew positions

◆ init()

type(cubicspline) function init ( real(dp), dimension(:), intent(in) x,
real(dp), dimension(:), intent(in) y,
real(dp), intent(in) s1,
real(dp), intent(in) sn )
Returns
Coefficients stored in type(CubicSpline)
Parameters
[in]xindependent grid points
[in]ycorresponding function values
[in]s1second derivative at x(1)
[in]snsecond derivative at x(n) (Natural spline: s1=sn=0)

References csplines::csplrep().

Here is the call graph for this function:

◆ integrate()

procedure, pass(csp) integrate ( real(dp), intent(in) xl,
real(dp), intent(in) xu,
class(cubicspline), intent(in) csp,
logical, intent(in), optional extrapolate )

Definite integral of a cubic spline function.

Todo
Testing when extrapolate is True
Parameters
[in]xlLower limit in the integral.
[in]xuUpper limit in the integral.
[in]cspInterpolating object
[in]extrapolateFlag signaling if we extrapolate outside interval
Returns
Value of integral

◆ roots()

procedure, pass(csp) roots ( class(cubicspline), intent(in) csp)

csplroots Computes the roots of the Spline approximation

Parameters
[in]cspSpline approximation to consider
Returns
Roots (zeros) of the spline function

Examples:

real(dp), dimension(:), allocatable :: zeros
zeros = csp%roots()
The documentation for this interface was generated from the following file: