NuMFor 9f2ab49 (2024-04-08)
Numerical (Modern) Fortran. Library for Simple Numerical computing
List of all members
qag Interface Reference

Globally adaptive integration routine without weights. More...

Detailed Description

Globally adaptive integration routine without weights.

The routine calculates an approximation 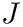$J$ to a definite integral

\[ J \approx I =\int_{a}^{b} f(x, args) dx \]

hopefully satisfying

\[ || I - J || \le \max ( epsabs, epsrel \cdot ||I|| ). \]

Parameters
[in]fThe function to integrate
[in]a(real) lower limit of integration
[in]b(real) upper limit of integration
[in]args(real, array, optional) extra arguments (if needed) to be passed to the function f
[out]IntVal(same kind as f) Approximation to integral
[in]epsabs(real, optional) Absolute accuracy requested. Default = 1.e-7
[in]epsrel(real, optional) Relative accuracy requested. Default = 1.e-5
[in]rule(character, optional) Choice of integration rule. Default = 'qk21'. Options are:
  • "qk15" -> 7 Gauss points, 15 Gauss-Kronrod points,
  • "qk21" -> 10 Gauss points, 21 Gauss-Kronrod points,
  • "qk31" -> 15 Gauss points, 31 Gauss-Kronrod points,
  • "qk41" -> 20 Gauss points, 41 Gauss-Kronrod points,
  • "qk51" -> 25 Gauss points, 51 Gauss-Kronrod points,
  • "qk61" -> 30 Gauss points, 61 Gauss-Kronrod points.
[out]abserr(real, optional) Estimation of absolute error achieved
[out]neval(integer, optional) Number of function evaluations performed
[out]ier(integer, optional) Error code
[in,out]info(optional) Information and workspace. Must be of type d_qp_extra for integration of real functions and of type c_qp_extra for integration of complex functions.

This is a simple globally adaptive integrator using the strategy of Aind (Piessens, 1973). The QAG algorithm is a simple adaptive integration procedure. The integration region is divided into subintervals, and on each iteration the subinterval with the largest estimated error is bisected. This reduces the overall error rapidly, as the subintervals become concentrated around local difficulties in the integrand. It is possible to choose between 6 pairs of Gauss-Kronrod quadrature formulae for the rule evaluation component. The pairs of high degree of precision are suitable for handling integration difficulties due to a strongly oscillating integrand.

Note
If present, info will store and use information about subdivisions, limits, errors, and status messages.

Example:

real(dp) :: Integ1
complex(dp) :: Integ2
real(dp), parameter :: epsrel = 1.e-3_8
intrinsic dsin
print "(A)", center(" Integrate sin(x) between 0 and pi ", 70, '-')
call qag(dsin, zero, m_pi, integ1)
print "(A)", '\int \sin(x) dx = '//str(integ1)//" (Difference="//str(abs(2 - integ1))//")"
! that prints:
!------------------ Integrate sin(x) between 0 and pi -----------------
! \int \sin(x) dx = 2 (Difference=0)
The documentation for this interface was generated from the following file: