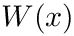Wrapper of (slightly modified) QUADPACK routines Description: Submodule Integrate. More...
Data Types | |
| interface | c_qp_extra |
| Type used to pass extra (optional) information with the integration routines. More... | |
| interface | d_qp_extra |
| Type used to pass extra (optional) information with the integration routines. More... | |
| interface | qag |
| Globally adaptive integration routine without weights. More... | |
| interface | qagp |
| Subroutine qagi is a globally adaptive, automatic interval subdivisions with epsilon extrapolation without weights for an infinite interval. More... | |
| interface | qags |
| Subroutine qags is a globally adaptive, automatic interval subdivisions with epsilon extrapolation without weights. More... | |
| interface | qawc |
| Subroutine qawc computes the Cauchy principal value. More... | |
| interface | qawf |
| qawf computes Fourier integrals over the interval [ A, +Infinity ). More... | |
| interface | qawo |
| Subroutine qawo is designed for integrands with an oscillatory factor,. More... | |
| interface | qaws |
| Subroutine qaws estimates integrals with algebraico-logarithmic endpoint singularities given by the weight function | |
| interface | qcheb |
| Subroutine qcheb computes the coefficients of the Chebyshev series expansion of degrees 12 and 24 of a function using a fast Fourier transform method. More... | |
| interface | qextr |
| Subroutine qextr carries out the Epsilon extrapolation algorithm. More... | |
| interface | qgk |
| Routine to perform the integration of a function by Gauss-Kronrod rule. More... | |
| interface | qk15w |
| Routine to perform the integration of a weighted function by 15-points Gauss-Kronrod rule. More... | |
| interface | qng |
| qng estimates an integral using non-adaptive integration. More... | |
Functions/Subroutines | |
| character(len=:) function, allocatable, public | qp_err_msg (ier) |
| qp_err_msg Returns the error message correspondig to a given code | |
Detailed Description
Wrapper of (slightly modified) QUADPACK routines Description: Submodule Integrate.
From QUADPACK original paper:
Introduction
QUADPACK is a Fortran subroutine package for the numerical computation of definite one-dimensional integrals. It originated from a joint project of R. Piessens and E. de Doncker (Appl. Math. and Progr. Div.- K.U.Leuven, Belgium), C. Ueberhuber (Inst. Fuer Math.-Techn.U.Wien, Austria), and D. Kahaner (Nation. Bureau of Standards- Washington D.C., U.S.A.).
All routines calculate approximations 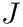
![\[ J \approx I := \int_{a}^{b} f(x, args) dx \]](form_32.png)
or integrals of weighted functions:
![\[ J \approx I := \int_{a}^{b} f(x) W(x) dx \]](form_33.png)
hopefully satisfying error conditions given by the user (epsabs, epsrel)
![\[ || I - J || \le \max ( \mathrm{epsabs}, \mathrm{epsrel} \cdot ||I|| ). \]](form_34.png)
Guidelines for the use of QUADPACK
Here it is not our purpose to investigate the question when automatic quadrature should be used. we shall rather attempt to help the user who already made the decision to use quadpack, with selecting an appropriate routine or a combination of several routines for handling his problem.
For both quadrature over finite and over infinite intervals, one of the first questions to be answered by the user is related to the amount of computer time he wants to spend, versus his -own- time which would be needed, for example, for manual subdivision of the interval or other analytic manipulations.
- The user may not care about computer time, or not be willing to do any analysis of the problem. especially when only one or a few integrals must be calculated, this attitude can be perfectly reasonable. in this case it is clear that either the most sophisticated of the routines for finite intervals, qags, must be used, or its analogue for infinite intervals, qagi. these routines are able to cope with rather difficult, even with improper integrals. this way of proceeding may be expensive. but the integrator is supposed to give you an answer in return, with additional information in the case of a failure, through its error estimate and flag. yet it must be stressed that the programs cannot be totally reliable.
The user may want to examine the integrand function. if bad local difficulties occur, such as a discontinuity, a singularity, derivative singularity or high peak at one or more points within the interval, the first advice is to split up the interval at these points. the integrand must then be examinated over each of the subintervals separately, so that a suitable integrator can be selected for each of them. if this yields problems involving relative accuracies to be imposed on -finite- subintervals, one can make use of qagp, which must be provided with the positions of the local difficulties. however, if strong singularities are present and a high accuracy is requested, application of qags on the subintervals may yield a better result.
for quadrature over finite intervals we thus dispose of qags and
- qng for well-behaved integrands,
- qag for functions with an oscillating behavior of a non specific type,
- qawo for functions, eventually singular, containing a factor cos(omega*x) or sin(omega*x) where omega is known,
- qaws for integrands with algebraico-logarithmic end point singularities of known type,
- qawc for cauchy principal values.
- Remarks
- On return, the info type
[d|c]_qp_extrain the last argument adaptive integrators contain information about the interval subdivision process and hence about the integrand behavior: the end points of the subintervals, the local integral contributions and error estimates, and eventually other characteristics. for this reason, and because of its simple globally adaptive nature, the routine qag in particular is well-suited for integrand examination. difficult spots can be located by investigating the error estimates on the subintervals.
for infinite intervals we provide only one general-purpose routine, qagi. it is based on the qags algorithm applied after a transformation of the original interval into (0,1). yet it may eventuate that another type of transformation is more appropriate, or one might prefer to break up the original interval and use qagi only on the infinite part and so on. these kinds of actions suggest a combined use of different quadpack integrators. note that, when the only difficulty is an integrand singularity at the finite integration limit, it will in general not be necessary to break up the interval, as qagi deals with several types of singularity at the boundary point of the integration range. it also handles slowly convergent improper integrals, on the condition that the integrand does not oscillate over the entire infinite interval. if it does we would advise to sum succeeding positive and negative contributions to the integral -e.g. integrate between the zeros- with one or more of the finite-range integrators, and apply convergence acceleration eventually by means of quadpack subroutine qext which implements the epsilon algorithm. such quadrature problems include the fourier transform as a special case. yet for the latter we have an automatic integrator available, qawf.
How to decide what routine to use.
If your integration region is finite:
- If you can factor the integrand as
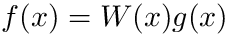
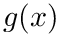
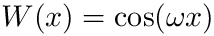
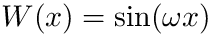
- Otherwise, if you can factor
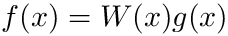
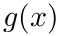
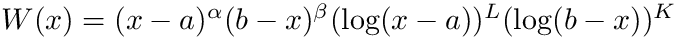
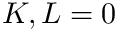
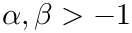
- Otherwise, if you can factor
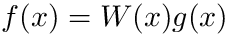
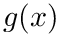
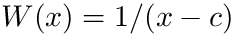
- Otherwise, if you do not care too much about possible inefficient use of computer time, and do not want to further analyze the problem, use qags().
- Otherwise, if the integrand is smooth, use qng() or qag().
- Otherwise, if there are discontinuities or singularities of the integrand or of its derivative, and you know where they are, split the integration range at these points and analyze each subinterval. You can also use
qagp, which is to be provided with the x-locations of the singularities or discontinuities. - Otherwise, if the integrand has end point singularities, use
qags. - Otherwise, if the integrand has an oscillatory behavior of nonspecific type, and no singularities, use qag() with rule="qk61".
- Otherwise, use qags().
Routines for an infinite region:
- If the integrand decays rapidly to zero, truncate the interval and use the finite interval decision tree.
- Otherwise, if the integrand oscillates over the entire infinite range, and the integral is a Fourier transform, use
qawf. - Or, if the integrand oscillates over the entire infinite range, but is not a Fourier transform, then sum the successive positive and negative contributions by integrating between the zeroes of the integrand. Apply convergence acceleration with
qextr. - Otherwise, if you are not constrained by computer time, and do not wish to analyze the problem further, use
qagi. - Otherwise, if the integrand has a non-smooth behavior in the range, and you know where it occurs, split off these regions and use the appropriate finite range routines to integrate over them. Then begin this tree again to handle the remainder of the region.
- Otherwise, truncation of the interval, or application of a suitable transformation for reducing the problem to a finite range may be possible. And you may also call
qagi.
Integrable functions
All routines described here may integrate functions with one of the following signatures:
- real function
f(x)of a real argumentx - complex function
f(x)of a real argumentx - real function
f(x,args)of real argumentsx, and arrayargs - complex function
f(x,args)of real argumentsx, and arrayargs
For functions that need extra arguments besides the integration variable x, the argument array must be passed to the integration routines.
There is also the possibility of using type(nf_rfunction) for real functions or type(nf_cfunction) for complex functions
Function/Subroutine Documentation
◆ qp_err_msg()
| character(len=:) function, allocatable, public qp_err_msg | ( | integer, intent(in) | ier | ) |
qp_err_msg Returns the error message correspondig to a given code
- Returns
- Error message
- Parameters
-
[in] ier Error code Examples: