NuMFor cf0f85d (2025-09-27)
Numerical (Modern) Fortran. Library for Simple Numerical computing
List of all members
qk15w Interface Reference

Routine to perform the integration of a weighted function by 15-points Gauss-Kronrod rule. More...

Detailed Description

Routine to perform the integration of a weighted function by 15-points Gauss-Kronrod rule.

This routine is non-automatic and approximates the integral of the function and its absolute value

\[ I= \int_{a}^{b} f(x) W(x) dx \]

Parameters
f(in) The function to integrate
w(in) The (real) weight function W(x)
p(in, real, array) extra arguments for the weight function
kp(in, integer) flag indicating the type of weight function
a(in, real) lower limit of integration
b(in, real) upper limit of integration
args(in, real, array, optional) extra arguments (if needed) to be passed to the function f
result(out, same kind as f) Approximation to integral I = integ(f(x), a, b), i.e: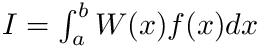 $ I =\int_{a}^{b} W(x) f(x) dx $
abserr(out, real) Estimation of error
resabs(out, same kind as f) Approximation to integral of absolute value of f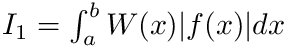 $ I_1 =\int_{a}^{b} W(x) |f(x)| dx $
resacs(out, real) Approximation to integral 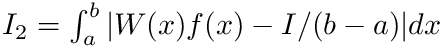$ I_2 =\int_{a}^{b} |W(x) f(x)-I/(b-a)| dx $

The routine returns the result of applying the m-point Kronrod (result I) rule obtained by optimal addition of abscissae to the n-point Gauss rule (result J), where 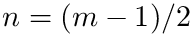$n=(m-1)/2$ .
The absolute error is evaluated as abserr=|I-J|.

The documentation for this interface was generated from the following file: