Subroutine qags is a globally adaptive, automatic interval subdivisions with epsilon extrapolation without weights. More...
Detailed Description
Subroutine qags is a globally adaptive, automatic interval subdivisions with epsilon extrapolation without weights.
The routine calculates an approximation 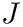
- Parameters
-
[in] f The function to integrate [in] a (real) lower limit of integration [in] b (real) upper limit of integration [in] args (real, array, optional) extra arguments (if needed) to be passed to the function f [out] IntVal (same kind as f) Approximation to integral [in] epsabs (real, optional) Absolute accuracy requested. Default = 1.e-7 [in] epsrel (real, optional) Relative accuracy requested. Default = 1.e-5 [in] gkrule (char(len=4), optional) Choice of integration rule Possible values are: 'qk15', 'qk21', 'qk31', 'qk41', 'qk51', 'qk61'. Default = 'qk21'. [out] abserr (real, optional) Estimation of absolute error achieved [out] neval (integer, optional) Number of function evaluations performed [out] ier (integer, optional) Error code [in,out] info (optional) Information and workspace. Must be of type d_qp_extra for integration of real functions and of type c_qp_extra for integration of complex functions
- Remarks
- (from gsl) The presence of an integrable singularity in the integration region causes an adaptive routine to concentrate new subintervals around the singularity. As the subintervals decrease in size the successive approximations to the integral converge in a limiting fashion. This approach to the limit can be accelerated using an extrapolation procedure. The QAGS algorithm combines adaptive bisection with the Wynn epsilon-algorithm to speed-up the integration of many types of integrable singularities.
Either or both limits of integration may be infinite. By default it uses a Gauss-Kronrod rule of 21 points for finite limits.
For infinite limits use nf_minf for "minus infinite" and nf_inf for "plus infinite". A 15-points Gauss-Kronrod rule will be used by default but it will be overriden by the argument gkrule.
The integration over the semi-infinite interval 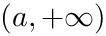
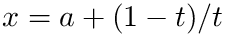
![$(0,1]$](form_10.png)
![\[ \int_{a}^{+\infty} dx f(x) = \int_0^1 dt f(a + (1-t)/t)/t^2
\]](form_97.png)
The integration over the semi-infinite interval 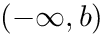
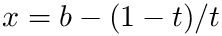
![$(0,1]$](form_10.png)
![\[ \int_{-\infty}^{b} dx f(x) = \int_0^1 dt f(b - (1-t)/t)/t^2
\]](form_98.png)
The integral over the infinite interval 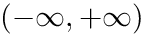
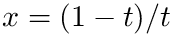
![$(0,1]$](form_10.png)
![\[\int_{-\infty}^{+\infty}dx f(x)=\int_0^1 dt\Big(f((1 - t) / t) + f(-(1 - t) / t) \Big) / t^2.\]](form_53.png)
Example:
The documentation for this interface was generated from the following file:
- /home/fiol/Trabajos/fortran/numfor/src/integrate/wquadpack.f90