NuMFor 9f2ab49 (2024-04-08)
Numerical (Modern) Fortran. Library for Simple Numerical computing
List of all members
qgk Interface Reference

Routine to perform the integration of a function by Gauss-Kronrod rule. More...

Detailed Description

Routine to perform the integration of a function by Gauss-Kronrod rule.

This routine is non-automatic and approximates the integral of the function and its absolute value

Parameters
[in]fThe function to integrate
[in]a(real) lower limit of integration
[in]b(real) upper limit of integration
[in]args(real, array, optional) extra arguments (if needed) to be passed to the function f
[out]IntVal(same kind as f) Approximation to integral I = integ(f(x), a, b), i.e: 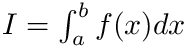$ I =\int_{a}^{b} f(x) dx $
[in]rule(character(len=4), optional) Choice of integration rule. Default = 'qk21'. Options are:
  • "qk15" -> 7 Gauss points, 15 Gauss-Kronrod points,
  • "qk21" -> 10 Gauss points, 21 Gauss-Kronrod points,
  • "qk31" -> 15 Gauss points, 31 Gauss-Kronrod points,
  • "qk41" -> 20 Gauss points, 41 Gauss-Kronrod points,
  • "qk51" -> 25 Gauss points, 51 Gauss-Kronrod points,
  • "qk61" -> 30 Gauss points, 61 Gauss-Kronrod points.
[out]abserr(real) Estimation of error
[out]resabs(same kind as f) Approximation to integral of absolute value of f 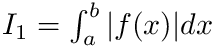$ I_1 =\int_{a}^{b} |f(x)| dx $
[out]resacs(real) Approximation to integral 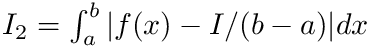$ I_2 =\int_{a}^{b} |f(x)-I/(b-a)| dx $

The routine returns the result of applying the m-point Kronrod (result I) rule given by arg rule by optimal addition of abscissae to the n-point Gauss rule (result J), where 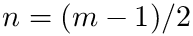$n=(m-1)/2$ .
The absolute error is evaluated as abserr=|I-J|.

The documentation for this interface was generated from the following file: