NuMFor 9f2ab49 (2024-04-08)
Numerical (Modern) Fortran. Library for Simple Numerical computing
List of all members
qawc Interface Reference

Subroutine qawc computes the Cauchy principal value. More...

Detailed Description

Subroutine qawc computes the Cauchy principal value.

\[ I= \int_{a}^{b} f(x) W(x) dx \]

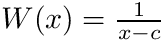
where $ W(x) = \frac{1}{x-c} $.

Parameters
[in]fThe function to integrate
[in]a(real) lower limit of integration
[in]b(real) upper limit of integration
[in]c(real) Point where lies the singularity
[in]args(real, array, optional) extra arguments (if needed) to be passed to the function f
[out]IntVal(same kind as f) Approximation to integral
[in]epsabs(real, optional) Absolute accuracy requested. Default = 1.e-7
[in]epsrel(real, optional) Relative accuracy requested. Default = 1.e-5
[out]abserr(real, optional) Estimation of absolute error achieved
[out]neval(integer, optional) Number of function evaluations performed
[out]ier(integer, optional) Error code
[in,out]info(optional) Information and workspace. Must be of type d_qp_extra for integration of real functions and of type c_qp_extra for integration of complex functions.
Note
As explained in gsl, the adaptive bisection algorithm of QAG is used, with modifications to ensure that subdivisions do not occur at the singular point $x = c$. When a subinterval contains the point $x = c$ or is close to it then a special 25-point modified Clenshaw-Curtis rule is used to control the singularity. Further away from the singularity the algorithm uses an ordinary 15-point Gauss-Kronrod integration rule.

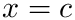
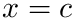
Example:

real(dp) :: Integ1
call qawc(fquad459, -1._dp, 5._dp, 0._dp, integ1)
print "(A)", 'integrate(1/(x(5 x^3 + 6), -1, 5)) = '//str(integ1)
! integrate(1/(x(5 x^3 + 6), -1, 5)) = -0.0899440069576
The documentation for this interface was generated from the following file: