NuMFor 9f2ab49 (2024-04-08)
Numerical (Modern) Fortran. Library for Simple Numerical computing
List of all members
qng Interface Reference

qng estimates an integral using non-adaptive integration. More...

Detailed Description

qng estimates an integral using non-adaptive integration.

The routine calculates an approximation 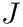$J$ to a definite integral

\[ J \approx I =\int_{a}^{b} f(x, args) dx \]

hopefully satisfying

\[ || I - J || \le \max ( epsabs, epsrel \cdot ||I|| ). \]

Parameters
[in]fThe function to integrate
[in]a(real) lower limit of integration
[in]b(real) upper limit of integration
[in]args(real, array, optional) extra arguments (if needed) to be passed to the function f
[out]IntVal(same kind as f) Approximation to integral
[in]epsabs(real, optional) Absolute accuracy requested. Default = 1.e-7
[in]epsrel(real, optional) Relative accuracy requested. Default = 1.e-5
[out]abserr(real, optional) Estimation of absolute error achieved
[out]neval(integer, optional) Number of function evaluations performed
[out]ier(integer optional) Error code

The routine is a simple non-adaptive automatic integrator, based on a sequence of rules with increasing degree of algebraic precision (Patterson, 1968). It applies the Gauss-Kronrod 10-point, 21-point, 43-point and 87-point integration rules in succession until an estimate of the integral is achieved within the desired absolute and relative error limits.

Example:

real(dp) :: Integ1
complex(dp) :: Integ2
intrinsic dsin
print "(A)", center(" Integrate sin(x) between 0 and pi ", 70, '-')
call qng(dsin, zero, m_pi, integ1)
print "(A)", '\int \sin(x) dx = '//str(integ1)//" (Difference="//str(abs(2 - integ1))//")"
! that prints:
!------------------ Integrate sin(x) between 0 and pi -----------------
! \int \sin(x) dx = 2 (Difference=0)
The documentation for this interface was generated from the following file: