qaws
Subroutine qaws estimates integrals with algebraico-logarithmic endpoint singularities given by the weight function 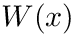
Detailed Description
Subroutine qaws estimates integrals with algebraico-logarithmic endpoint singularities given by the weight function 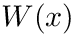
![\[ I= \int_{a}^{b} f(x) W(x) dx \]](form_54.png)
- Parameters
-
[in] f The function to integrate [in] a (real) lower limit of integration [in] b (real) upper limit of integration [in] alfa (real) parameter of the weight function [in] beta (real) parameter of the weight function [in] flgw (integer) flag indicating the kind of weight function used: - flgw = 1
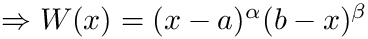
- flgw = 2
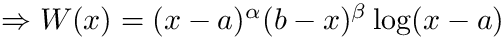
- flgw = 3
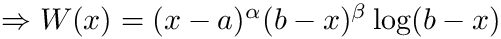
- flgw = 4
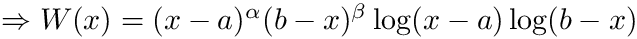
[in] args (real, array, optional) extra arguments (if needed) to be passed to the function f [out] IntVal (same kind as f) Approximation to integral [in] epsabs (real, optional) Absolute accuracy requested. Default = 1.e-7 [in] epsrel (real, optional) Relative accuracy requested. Default = 1.e-5 [out] abserr (real, optional) Estimation of absolute error achieved [out] neval (integer, optional) Number of function evaluations performed [out] ier (integer, optional) Error code [in,out] info (optional) Information and workspace. Must be of type d_qp_extra for integration of real functions and of type c_qp_extra for integration of complex functions. - flgw = 1
Example:
real(dp) :: Integ1
real(dp) :: alfa, beta
integer :: flgw
alfa = 0._dp
beta = 0._dp
flgw = 2 ! weight function => log(x-a)^alfa = log(x)
! fquad458 = 1/(1 + \ln(x)^{2})^{2}
call qaws(fquad458, zero, 1._dp, alfa, beta, flgw, integ1)
print "(A)", 'integrate(log(x)/(1 + ln(x)^{2})^{2}, 0, 1) = '//str(integ1)
! integrate(log(x)/(1 + ln(x)^{2})^{2}, 0, 1) = -0.1892750041577
The documentation for this interface was generated from the following file:
- /home/fiol/Trabajos/fortran/numfor/src/integrate/wquadpack.f90