NuMFor cf0f85d (2025-09-27)
Numerical (Modern) Fortran. Library for Simple Numerical computing
List of all members
qawf Interface Reference

qawf computes Fourier integrals over the interval [ A, +Infinity ). More...

Detailed Description

qawf computes Fourier integrals over the interval [ A, +Infinity ).

\[ I= \int_{a}^{\infty} f(x) W(x) dx \]

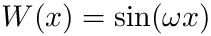
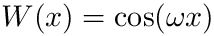
where $ W(x) = \sin(\omega x)$ or $ W(x) = \cos(\omega x)$.

Parameters
[in]fThe function to integrate
[in]a(real) lower limit of integration
[in]omega(real) factor in the weight function
[in]flgw(integer) flag indicating if weight is cosine (flgw=1)
[in]args(real, array, optional) extra arguments (if needed) to be passed to the function f
[out]IntVal(same kind as f) Approximation to integral
[in]epsabs(real, optional) Absolute accuracy requested. Default = 1.e-7
[out]abserr(real, optional) Estimation of absolute error achieved
[out]neval(integer, optional) Number of function evaluations performed
[out]ier(integer, optional) Error code
[in,out]info(optional) Information and workspace. Must be of type d_qp_extra for integration of real functions and of type c_qp_extra for integration of complex functions.
Note
The integral is computed using the qawo subroutine over each of the subintervals:

\begin{align*} C_1 &= [a,a+c] \\ C_2 &= [a+c,a+2c] \\ \vdots & \\ C_k &= [a+(k-1)c,a+kc] \end{align*}

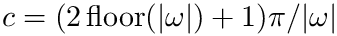
where $ c = (2 \, \mathrm{floor}(|\omega|) + 1) \pi/|\omega| $ is chosen to span an odd number of periods.

Example:

real(dp) :: Integ1
! Fourth argument, flgw=1 => weight function is cosine
! fquad457 => 1/\sqrt(x)
call qawf(fquad457, zero, m_pi / 2, 1, integ1)
print "(A)", 'integrate(cos(pi x /2 ) / sqrt(x), x, 0, inf ) = '//str(integ1)
! integrate(cos(pi x /2 ) / sqrt(x), x, 0, inf ) = 0.9999999999321
The documentation for this interface was generated from the following file: