NuMFor 9f2ab49 (2024-04-08)
Numerical (Modern) Fortran. Library for Simple Numerical computing
List of all members
qcheb Interface Reference

Subroutine qcheb computes the coefficients of the Chebyshev series expansion of degrees 12 and 24 of a function using a fast Fourier transform method. More...

Detailed Description

Subroutine qcheb computes the coefficients of the Chebyshev series expansion of degrees 12 and 24 of a function using a fast Fourier transform method.

\[ f(x) = \sum_{k} (\mathrm{Cheb}(k) T_{k-1}(x) , \]

where $ T_{k}(x)$ is the Chebyshev polynomial of degree k.

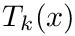
Reference: Robert Piessens, Elise de Doncker-Kapenger, Christian Ueberhuber, David Kahaner, QUADPACK, a Subroutine Package for Automatic Integration, Springer Verlag, 1983. (Section 2.2.3.2)

Parameters
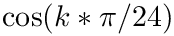
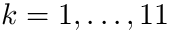
[in]x(real, dimension(11)) values of $ \cos(k*\pi/24)$, for $k = 1, \dots, 11 $
[in,out]fval(real or complex, dimension(25))
[out]cheb12(real or complex) the Chebyshev coefficients for degree 12
[out]cheb24(real or complex) the Chebyshev coefficients for degree 24
The documentation for this interface was generated from the following file: