Normal random distribution The normal probability distribution located at 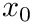$x_{0}$ and standard deviation $\sigma$ , is given by. More...

Data Types
interface	ran_gaussian_pdf
	This function computes the probability density function (pdf) p(x) at x for a Gaussian distribution with standard deviation `scale`, using the formula given above. More...

interface	random_normal
	Fills a scalar or array with random numbers following a normal (gaussian) distribution. More...

interface	random_standard_normal
	Convenience routine. Fills a scalar or array with random numbers following a standard normal (gaussian) distribution. Equivalently to random_normal() with `scale=1` and `loc=0`. More...

interface	rng_normal
	Functions returning a variate x with normal probability. More...

interface	rng_normal2
	Functions returning a variate x with normal probability. More...

Functions/Subroutines
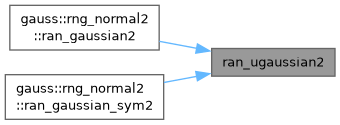
real(dp) function, public	ran_ugaussian2 ()
	Computes a Gaussian random variate, with mean zero and standard deviation `sigma=1`.

Detailed Description

Normal random distribution The normal probability distribution located at 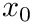$x_{0}$ and standard deviation $\sigma$ , is given by.

$p(x) dx = {1 \over \sqrt{2 \pi \sigma^2}} \exp (-(x-x_{0})^2 / 2\sigma^2) dx$

Function/Subroutine Documentation

real(dp) function, public ran_ugaussian2

Computes a Gaussian random variate, with mean zero and standard deviation sigma=1.

Note: This version caches the last unused value. It should be faster but will have problems in multi-threaded programs

Here is the caller graph for this function: