NuMFor 9f2ab49 (2024-04-08)
Numerical (Modern) Fortran. Library for Simple Numerical computing
Data Types | Functions/Subroutines
fitpack Module Reference
Polynomials, Interpolation, and fitting

fitpack provides a framework for fitting and interpolation using B-Splines. Description: Submodule interpolate More...

Data Types

interface  splev
 splev Computes a B-spline or its derivatives. More...
 
interface  splint
 splint Evaluates the definite integral of a B-spline. More...
 
type  univspline
 Type used to keep all information on spline fitting. More...
 

Functions/Subroutines

subroutine, public splprep (x, u, tck, w, ulim, k, task, upar, s, t, per, ier)
 splprep Computes the B-spline representation of an N-dimensional curve.
 
subroutine, public splrep (x, y, w, xb, xe, k, task, s, t, per, tck, ier)
 splrep Finds the B-spline representation of 1-D curve. Given the set of data points (x[i], y[i]) determine a smooth spline approximation of degree k on the interval xb <= x <= xe.
 
real(dp) function, dimension(:), allocatable, public splroot (tck)
 splroot Computes the roots of a cubic B-spline.
 

Detailed Description

fitpack provides a framework for fitting and interpolation using B-Splines. Description: Submodule interpolate

It uses routines from a slightly cleaned-up f90 version of FITPACK by P. Diercxx

Todo
Next Steps:
  • Add routines for ndimensional curves
  • Reorganize the files on fitpack (may be merging some of them)

Data Type Documentation

◆ fitpack::univspline

type fitpack::univspline

Type used to keep all information on spline fitting.

Class Members
real(dp), dimension(:), allocatable c coefficients
real(dp) fp weighted sum of squared residuals of the spline approximation returned.
integer, dimension(:), allocatable iwrk
integer k
real(dp), dimension(:), allocatable t knots
real(dp), dimension(:), allocatable wrk

Function/Subroutine Documentation

◆ splprep()

subroutine, public splprep ( real(dp), dimension(:, :), intent(in) x,
real(dp), dimension(:), intent(inout) u,
type(univspline), intent(out) tck,
real(dp), dimension(size(x(1, :))), intent(in), optional, target w,
real(dp), dimension(2), intent(inout), optional ulim,
integer, intent(in), optional k,
integer, intent(in), optional task,
logical, intent(in), optional upar,
real(dp), intent(in), optional s,
real(dp), dimension(:), intent(in), optional t,
logical, intent(in), optional per,
integer, intent(out), optional ier )

splprep Computes the B-spline representation of an N-dimensional curve.

Given a list of N rank-1 arrays, x, which represent a curve in N-dimensional space parametrized by u, find a smooth approximating spline curve g(u). Uses the routine parcur from (slightly modified) FITPACK.

Parameters
[in]x2D-Array representing the curve in an n-dimensional space
[in,out]uAn array with parameters. The routine will fill it if upar is False or not present.
[in]wStrictly positive rank-1 array of weights the same size as u.
[in,out]ulimLower and upper limits of the interval to approximate (ulim(1) <= u(1) and ulim(2) >= u(m) )
[in]kThe degree of the spline fit. It is recommended to use cubic splines. Even values of k should be avoided especially with small s values. 1 <= k <= 5
[in]task{1, 0, -1},\
  • If task==0 find t and c for a given smoothing factor, s.
  • If task==1 find t and c for another value of the smoothing factor, s. There must have been a previous call with task=0 or task=1 for the same set of data (it will be stored an used internally)
  • If task==-1 find the weighted least square spline for a given set of knots t. These should be interior knots as knots on the ends will be added automatically
[in]sA smoothing condition. The amount of smoothness is determined by satisfying the conditions:
sum((w * (y - g))**2) <= s where g(x) is the smoothed interpolation of (x,y).
The user can use s to control the tradeoff between closeness and smoothness of fit. Larger s means more smoothing while smaller values of s indicate less smoothing. Recommended values of s depend on the weights, w.
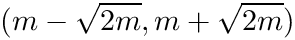
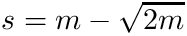
If the weights represent the inverse of the standard-deviation of y, then a good s value should be found in the range $ (m-\sqrt{2 m},m+\sqrt{2 m})$ where m is the number of datapoints in x, y, and w. default : $ s= m-\sqrt{2 m}$ if weights are supplied. s = 0.0 (interpolating) if no weights are supplied.
[in]tInput knots (interior knots only) needed for task = -1. If given then task is automatically set to -1.
[in]uparFlag indicating if u is given or must be automatically calculated. Default .False.
[in]perFlag indicating if data are considered periodic
[out]tckCoefficients, knots, and additional information for interpolation/fitting.
On output the following values of tck will be set:
  • c: coefficients
  • t: knots
  • k: order of splines.
  • wrk, iwrk: workspace for internal use only
  • fp: weighted sum of squared residuals

For tasks -1, or 1, on input the user may provide values for: wrk and iwrk: (but are usually set by a previous call)

Parameters
[out]ierError code

Examples:

! After setting data in x
! interpolate: (step one) Create interpolation and parameters u
call splprep(x, u, tck, s=s)
! interpolate: (step two) Apply to points u
call splev(u, tck, new_points)

Full example in Submodule interpolate

◆ splrep()

subroutine, public splrep ( real(dp), dimension(:), intent(in) x,
real(dp), dimension(size(x)), intent(in) y,
real(dp), dimension(size(x)), intent(in), optional w,
real(dp), intent(in), optional xb,
real(dp), intent(in), optional xe,
integer, intent(in), optional k,
integer, intent(in), optional task,
real(dp), intent(in), optional s,
real(dp), dimension(:), intent(in), optional t,
logical, intent(in), optional per,
type(univspline), intent(out) tck,
integer, intent(out), optional ier )

splrep Finds the B-spline representation of 1-D curve. Given the set of data points (x[i], y[i]) determine a smooth spline approximation of degree k on the interval xb <= x <= xe.

Parameters
[in]xValues of independent variable
[in]yThe data points y=f(x)
[in]wStrictly positive rank-1 array of weights the same size as x and y. The weights are used in computing the weighted least-squares spline fit. If the errors in the y values have standard-deviation given by the vector d, then w should be 1/d.
[in]xbLower limit of the interval to approximate (xb <= x(1))
[in]xeUpper limit of the interval to approximate (xe >= x(size(x))).
[in]kThe degree of the spline fit. It is recommended to use cubic splines. Even values of k should be avoided especially with small s values. 1 <= k <= 5
[in]task{1, 0, -1},
  • If task==0 find t and c for a given smoothing factor, s.
  • If task==1 find t and c for another value of the smoothing factor, s. There must have been a previous call with task=0 or task=1 for the same set of data (it will be stored an used internally)
  • If task==-1 find the weighted least square spline for a given set of knots t. These should be interior knots, as knots on the ends will be added automatically
[in]sA smoothing condition. The amount of smoothness is determined by satisfying the conditions:
sum((w * (y - g))**2) <= s where g(x) is the smoothed interpolation of (x,y). The user can use s to control the tradeoff between closeness and smoothness of fit. Larger s means more smoothing while smaller values of s indicate less smoothing. Recommended values of s depend on the weights, w.
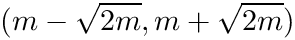
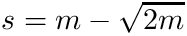
If the weights represent the inverse of the standard-deviation of y, then a good s value should be found in the range $ (m-\sqrt{2 m},m+\sqrt{2 m})$ where m is the number of datapoints in x, y, and w. default : $ s= m-\sqrt{2 m}$ if weights are supplied. It will use s = 0.0 (interpolating) if no weights are supplied.
[in]tInput knots (interior knots only) for task = -1. If given then task is automatically set to -1.
[in]perFlag indicating if data are considered periodic
[out]tckCoefficients, knots, and additional information for interpolation/fitting. On output the following values will be set:
  • c: coefficients
  • t: knots
  • k: order of splines.
  • wrk, iwrk: workspace arrays, for internal use only
  • fp: weighted sum of squared residuals On input, for tasks -1, 1 the user may provide values for: wrk, iwrk: For tasks. (but usually are set by a previous call)
[out]ierFlag of status at output

Examples:

! After setting data in x
! interpolate: (step one) Create interpolation and parameters u
call splrep(x, y, tck=tck, s=s)
! interpolate: (step two) Apply to points u
call splev(xnew, tck, ynew)

Full example in Submodule interpolate

◆ splroot()

real(dp) function, dimension(:), allocatable, public splroot ( type(univspline), intent(in) tck)

splroot Computes the roots of a cubic B-spline.

Returns
Array with the roots of the spline
Parameters
[in]tckUnivSpline object with knots and coefficients of spline