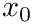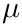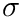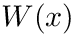Here are the data types with brief descriptions:

[detail level 12]

▼Marray_utils	This module provides convenience routines to operate or get information on arrays
Csave_array	Save_array Stores an 1D or 2D array to file or stdout
▼Mbasic	This module will provide some basic convenience routines Description
Ctimer	Simple timer. Holds start-time, stop-time, and time-difference
▼Mcsplines	Csplines implements interpolation using cubic splines Description: Submodule interpolate
Ccsplev	Csplev Performs a spline interpolation in a point or in a table
Ccsplevder	Csplev Performs a spline interpolation in a point or in a table
Ccubicspline	Type used to keep all information on splines
▼Mexponential	Exponential random distribution The exponential probability distribution located at $x_{0}$ and mean $\mu$ , is given by
Cran_exponential_pdf	This function computes the probability density p(x) at x for an exponential distribution
Crandom_exponential	Fills a scalar or array with random numbers following an exponential distribution
▼Mfitpack	Fitpack provides a framework for fitting and interpolation using B-Splines. Description: Submodule interpolate
Csplev	Splev Computes a B-spline or its derivatives
Csplint	Splint Evaluates the definite integral of a B-spline
Cunivspline	Type used to keep all information on spline fitting
▼Mfstring	Module defining the `fStr` object and its methods. Description
Cfstr	This type defines a string class, with its methods
▼Mfunc_integ	Definition of integrable functions Description: Submodule Integrate
Cnf_cfunction	Type to encapsulate complex functions and extra arguments
Cnf_rfunction	Type to encapsulate real functions and extra arguments
▼Mgauss	Normal random distribution The normal probability distribution located at $x_{0}$ and standard deviation $\sigma$ , is given by
Cran_gaussian_pdf	This function computes the probability density function (pdf) p(x) at x for a Gaussian distribution with standard deviation `scale`, using the formula given above
Crandom_normal	Fills a scalar or array with random numbers following a normal (gaussian) distribution
Crandom_standard_normal	Convenience routine. Fills a scalar or array with random numbers following a standard normal (gaussian) distribution. Equivalently to random_normal() with `scale=1` and `loc=0`
Crng_normal	Functions returning a variate x with normal probability
Crng_normal2	Functions returning a variate x with normal probability
▼Mhistograms	The module `histograms` provides infrastructure for the calculation of histograms. i.e: a count of frequency
Chistog	Type histogram holds the data from an histogram
▼Mpolynomial	Polynomials provides a framework for simple (and quite naive) work with polynomials Further description in Submodule interpolate
Cpolyval	Computes the value of the polynomial when applied to a number or list of numbers
▼Mqadaptive	Globally adaptive Simpson integrator. Description: Submodule Integrate
Ciads	Integration by Adaptive Simpson method of a function by a globally adaptive strategy, using a Simpson rule
Ciadsi	Integration by Adaptive Simpson method of a function on a semi-infinite interval, based on iads()
▼Mqsimpson	Routines for trapezoid and simpson integration of both sampled data and functions. Description: Submodule Integrate
Csimps	Routines for integration of sampled values or functions by using Simpson rule
Ctrapz	Routine for integration of sampled values or functions by using the trapezoid rule
▼Mqtanhsinh	Implementation of tanh-sinh integration method. Description: Submodule Integrate
Cqnthsh	Subroutine `qnthsh` implements integration by tanh-sinh method
▼Mquadpack	Wrapper of (slightly modified) QUADPACK routines Description: Submodule Integrate
Cc_qp_extra	Type used to pass extra (optional) information with the integration routines
Cd_qp_extra	Type used to pass extra (optional) information with the integration routines
Cqag	Globally adaptive integration routine without weights
Cqagp	Subroutine qagi is a globally adaptive, automatic interval subdivisions with epsilon extrapolation without weights for an infinite interval
Cqags	Subroutine qags is a globally adaptive, automatic interval subdivisions with epsilon extrapolation without weights
Cqawc	Subroutine qawc computes the Cauchy principal value
Cqawf	Qawf computes Fourier integrals over the interval [ A, +Infinity )
Cqawo	Subroutine qawo is designed for integrands with an oscillatory factor,
Cqaws	Subroutine qaws estimates integrals with algebraico-logarithmic endpoint singularities given by the weight function
Cqcheb	Subroutine qcheb computes the coefficients of the Chebyshev series expansion of degrees 12 and 24 of a function using a fast Fourier transform method
Cqextr	Subroutine qextr carries out the Epsilon extrapolation algorithm
Cqgk	Routine to perform the integration of a function by Gauss-Kronrod rule
Cqk15w	Routine to perform the integration of a weighted function by 15-points Gauss-Kronrod rule
Cqng	Qng estimates an integral using non-adaptive integration
▼Mrandom
Crandom_real_pos	Function returning a real number in the open interval (0,1)
Crandom_seed	Initialize the random number generator
▼Msorting	Sort provides a framework for searching elements and sorting arrays
Csearchsorted	Searchsorted: Find index where an element should be inserted in an array to maintain order
▼Mstrings	This module defines functions to manipulate strings of characters. Description
Cstr	`str()` converts a number (integer or real) to a string
▼Muniform	Uniform Random distribution Description: randist
Crandom_sample	Uniform Random distributions Fills a scalar or array with random numbers in the half-open interval [0, 1)
Crandom_uniform	Fills a scalar or array with random numbers in the half-open interval [low, high)
Crng_state	Rng_state holds the state of the generator